THE MOVING COIL GALVANOMETER
Galvanometer is an electromechanical instrument which is used for the detection of electric currents through electric circuits. Being a sensitive instrument, Galvanometer can not be used for the measurement of heavy currents. However we can measure very small currents by using galvanometer but the primary purpose of galvanometer is the detection of electric current not the measurement of current
WORKING PRINCIPLE
| |
| A current carrying conductor placed in a magnetic field experiences a torque | |
Construction
The concave or cylindrical pole pieces ensure that the plane of coil is parallel to B thus (cosq = 1 and sina = 1) in the expression t = NIBA cosq and t = NIBA sina .
The whole arrangement is enclosed in non-magnetic case, which is provided with leveling screws. The torsion head is connected to terminal T1. The galvanometer can be connected to the circuit through terminals T1 and T2.
WORKING
When a current is passed through the coil in the direction PQRS, then the coil experiences a torquet = NIBA sina
Since the magnified field is radial the plane of the coil is parallel to the magnetic field
 such that a = 90o and hence t = NIBA.
such that a = 90o and hence t = NIBA.The coil rotates and the phosphor bronze strip gets twisted. As a result a restoring torque comes into play trying to restore the coil back to original position.
If f be the twist produced in the strip and C be the restoring torque per unit twist then the restoring torque = Cf.
In equilibrium,
where G is the galvanometer constant.

This shows that galvanometer has a linear scale and detects the presence of current
Note:
Current sensitivity of galvanometer is the deflection produced for a unit current flowing through it. i.e.,
Voltage sensitivity is the deflection produced for a unit voltage applied across the two terminals of the galvanometer
TORQUE ON A CURRENT CARRYING LOOP IN UNIFORM MAGNETIC FIELD
Consider a rectangular coil with sides of length a and b placed in a magnetic field of flux density B and free to rotate about an axis perpendicular to the paper, as shown in Figure . A current of I Amps flows in the coil. 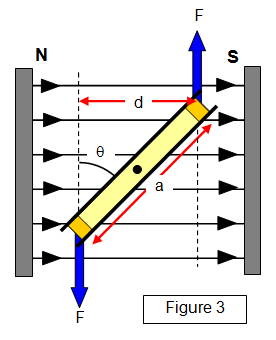
The field exerts a force on the sides b given by
Force (F) on side length b = BNIb
where N is the number of turns on the coil.
If the perpendicular to the coil is at an angle θ to the field direction, then the torque exerted on the coil is Fd where d = a sin q.
Therefore the torque C is given by:
Torque (C) on the coil = BANI sinθ
where A = ab, the area of one face of the coil.
The maximum torque occurs when the plane of the coil is lying along the field lines (θ = 90o and sin q = 1). At this point, shown in Figure 2(a),
The minimum value of the torque is zero, when θ = 0.
BEST OF LUCK GUYS......
VIKAS BHATI


No comments:
Post a Comment